About my research
I am particularly interested in theories for the mechanism of economic agglomeration and the corresponding empirical analyses. I focus on agglomeration since it is a representative form of economic location today. More than 70-80% of production and population concentrate in a few percent of the area in most developed countries and regions. Economic agglomerations, or cities, exhibit highly regular spatial patterns, and these patterns are quite similar across countries and regions. Typically, population size, industrial composition, and spatial patterns of cities exhibit spatial fractal structure. The structural regularity has been persistent despite various large scale policy implementations (e.g., highway network development) to influence the economic location.
Selected publications
Centrality bias in inter-city trade. Regional Science and Urban Economics 109:104060, 2024. DOI: 10.1016/j.regsciurbeco.2024.104060 (with J. Wrona)
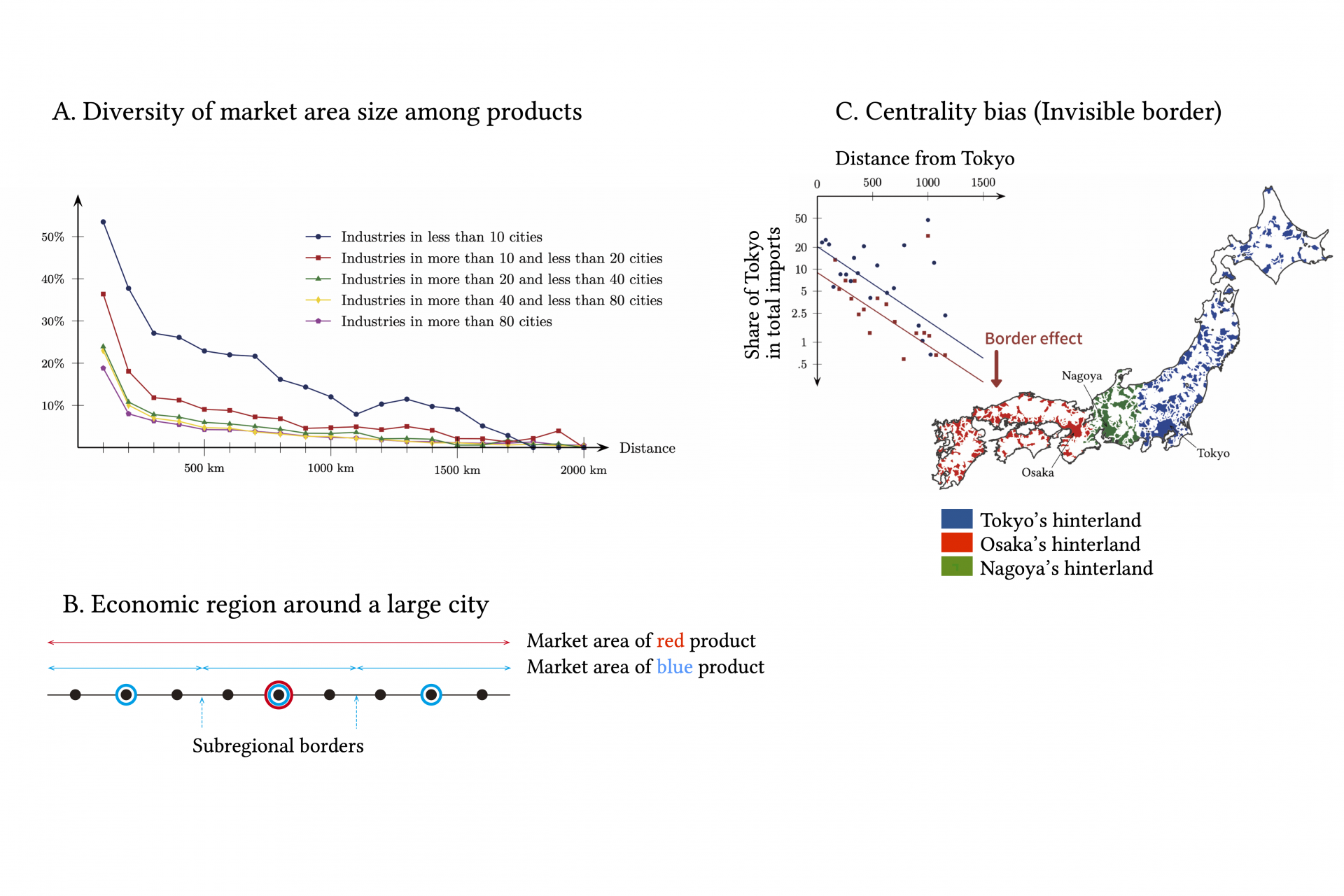 This paper demonstrates the formation of economic regions using intercity trade data of Japan and the US. In a regional economy, a nested city arrangement is realized. Small cities surround large cities, and even smaller cities further surround each of these small cities. The so-called central place theory explains such city arrangements in terms of the spatial coordination of many industries. For example, in industries with high fixed costs, large markets are required for firms to enter. Thus, firms are located only in a few cities, and goods and services are widely supplied. On the other hand, in industries with low fixed costs, even small markets can suffice for firms to enter, so they are found in many cities. Analysis of trade data between cities confirms that industries located in fewer cities export more extensively (Fig. A). While the spatial frequency of appearance varies among industries, different industries tend to attract each other and be located in a common city because many goods and services share consumers, directly and indirectly. For example, a city with a theater also has a movie theater; a city with a movie theater also has a bakery. (Conversely, a city with a bakery does not necessarily have a movie theater. A city with a movie theater does not necessarily have a theater.) A city’s industrial diversity and population size correlate so that cities with many industries tend to be large. In contrast, cities with only a few industries tend to be small. Fig. B summarizes the resulting industrial location and urban layout. Central place theory asserts that the market area of industries specific to a given city constitutes an economic region of the city, as indicated in Fig. B. Analysis of inter-city trade data confirms the presence of invisible trade barriers at the approximated regional borders. The exports from a large city (central place) decline by two-thirds to half in crossing the border in addition to the decline over distance (Fig. C). Mori et al. (2020) show that the same set of regions exhibit common power law for city size distributions.
This paper demonstrates the formation of economic regions using intercity trade data of Japan and the US. In a regional economy, a nested city arrangement is realized. Small cities surround large cities, and even smaller cities further surround each of these small cities. The so-called central place theory explains such city arrangements in terms of the spatial coordination of many industries. For example, in industries with high fixed costs, large markets are required for firms to enter. Thus, firms are located only in a few cities, and goods and services are widely supplied. On the other hand, in industries with low fixed costs, even small markets can suffice for firms to enter, so they are found in many cities. Analysis of trade data between cities confirms that industries located in fewer cities export more extensively (Fig. A). While the spatial frequency of appearance varies among industries, different industries tend to attract each other and be located in a common city because many goods and services share consumers, directly and indirectly. For example, a city with a theater also has a movie theater; a city with a movie theater also has a bakery. (Conversely, a city with a bakery does not necessarily have a movie theater. A city with a movie theater does not necessarily have a theater.) A city’s industrial diversity and population size correlate so that cities with many industries tend to be large. In contrast, cities with only a few industries tend to be small. Fig. B summarizes the resulting industrial location and urban layout. Central place theory asserts that the market area of industries specific to a given city constitutes an economic region of the city, as indicated in Fig. B. Analysis of inter-city trade data confirms the presence of invisible trade barriers at the approximated regional borders. The exports from a large city (central place) decline by two-thirds to half in crossing the border in addition to the decline over distance (Fig. C). Mori et al. (2020) show that the same set of regions exhibit common power law for city size distributions.
Common power laws for cities and spatial fractal structures. Proceedings of the National Academy of Sciences of the United States of America 117(12) 6469-6475, 2020. DOI:10.1073/pnas.1910314117. (with T. E. Smith & W.-T. Hsu) DOI:10.1073
It is a known fact that in many countries, city-size distribution approximately follows a power law. This paper uses data from six countries, including Japan and the US, to recursively observe such regularity formation at the national and regional levels and smaller regions within each region (click the panel above). While the power-law coefficient varies from country to country, countries share a common structure that the spatial arrangement of cities in each region is generally similar to the arrangement of cities at the country level, with small cities surrounding the central metropolis. This fact is interesting as a phenomenon and has important policy implications since city size strongly correlates with various other socio-economic indicators such as industrial diversity, household income, and educational level. Which city will grow is a musical chairs game, where it is unlikely for the number of chairs to increase or the spacing to change. Inequality among cities tends to be maintained. In the first place, the fact that the city-size distribution follows the power law at the national level may be because the country’s territory is also the result of endogenous regional formation. The central city cannot grow unboundedly, as the level of technology bounds its scale, which in turn constrains the country’s size. The reason why huge countries such as the Roman Empire and the Chinese dynasty did not remain may be closely related to the fractal structure with the power-law identified in this study. In a related study by Mori and Wrona (2021), we show that the regions constituting the fractal structure are relatively autonomous in inter-city trade. In particular, we identify invisible trade barriers at the regional borders.
On the spatial scale of industrial agglomerations. Journal of Urban Economics 89: 1-20, 2015. DOI: 10.1016/j.jue.2015.01.006. (with T. E. Smith) LINK
The number-average size rule: A new empirical relationship between industrial location and city size. Journal of Regional Science 48(1): 165-211, 2008. DOI: 10.1111/j.1467-9787.2008.00550.x (with K. Nishikimi, T.E. Smith) LINK
A divergent statistic for industrial localization. Review of Economics & Statistics 87(4): 635-651, 2005. DOI: 10.1162/003465305775098170 (with K. Nishikimi, T.E. Smith) LINK
Skills, agglomeration, and segmentation. European Economic Review 49(1): 201-225, 2005. DOI: 10.1016/S0014-2921(03)00018-7 (with A. Turrini) LINK
On the evolution of hierarchical urban systems. European Economic Review 43(2): 209-251, 1999; DOI: 10.1016/S0014-2921(98)00066-X (with M. Fujita, P. Krugman) LINK
Recent discussion papers and lectures
Urban Economics Association – Summer School Lecture, 2023, on “Endogenous multimodal agglomeration.” [LINK]
Lecture slides for Urban Economics Association Summer School at Université du Québec à Montréal (UQAM), May 29th-31st, 2023.
Origin of power laws and their spatial fractal structure for city-size distributions. arXiv:2207.05346, 2022 (with T. Akamatsu, Y. Takayama, M. Osawa).
City-size distributions follow an approximate power law in various countries despite high volatility in relative city sizes over time. Our empirical evidence for the United States indicates that the scaling law stems from a spatial fractal structure owing to the coordination of industrial locations. While the locations of individual industries change considerably over time, there is a persistent pattern in that more localized industries at a given time are found only in larger cities. The spatial organization of cities exhibits a hierarchical structure in which larger cities are spaced apart to serve as centers for surrounding smaller cities, generating a recursive pattern across different spatial scales. In our theoretical replication of the observed regularities, diversity in scale economy among industries induces diversity in their location pattern, which translates into diversity in city size via spatial coordination of industries and population. The city-size power law is a generic feature of Monte-Carlo samples of stationary states resulting from the spontaneous spatial fractal structure in the hypothetical economy. The identified regularities reveal constraints on feasible urban planning at each regional scale. The success or failure of place-based policies designed to take advantage of individual cities’ characteristics should depend on their spatial relationships with other cities, subject to the nationwide spatial fractal structure.
Collaborative knowledge exchange promotes innovation. arXiv:2210.01392, 2022 (with J. Newton and S. Sakaguchi)
Considering collaborative patent development, we provide micro-level evidence for innovation through exchanges of differentiated knowledge. Knowledge embodied in a patent is proxied by word pairs appearing in its abstract, while novelty is measured by the frequency with which these word pairs have appeared in past patents. Inventors are assumed to possess the knowledge associated with patents in which they have previously participated. We find that collaboration by inventors with more mutually differentiated knowledge sets is likely to result in patents with higher novelty.
Spatial scale of agglomeration and dispersion: Number, spacing, and the spatial extent of cities. arXiv: 1912.05113, 2024 (with T. Akamatsu, M. Osawa, Y. Takayama) LINK